Нелинейная регрессия в Excel

Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ.

Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.

Основными типами нелинейных регрессий являются:

полиномиальные (квадратичная, кубическая);
гиперболическая;
степенная;
показательная;
логарифмическая.

Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.

В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А), если она находится в промежутке <8…10%, значит модель достаточно точна.

На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.

У нас имеется таблица продаж автомобилей за промежуток 15 лет (обозначим его X), количество шагов измерений будет аргумент n, также имеется выручка за эти периоды (обозначим её Y), нам нужно спрогнозировать какова будет выручка в дальнейшем. Построим следующую таблицу:

Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax²+bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов - a, b, c. Он приведёт к системе алгебраических уравнений вида:

Для решения этой системы воспользуемся, к примеру, методом Крамера. Видим, что входящие в систему суммы являются коэффициентами при неизвестных. Для их вычисления добавим в таблицу несколько столбцов (D,E,F,G,H) и подпишем соответственно смыслу вычислений - в столбце D возведём x в квадрат, в E в куб, в F в 4 степень, в G перемножим показатели x и y, в H возведём x в квадрат и перемножим с y.

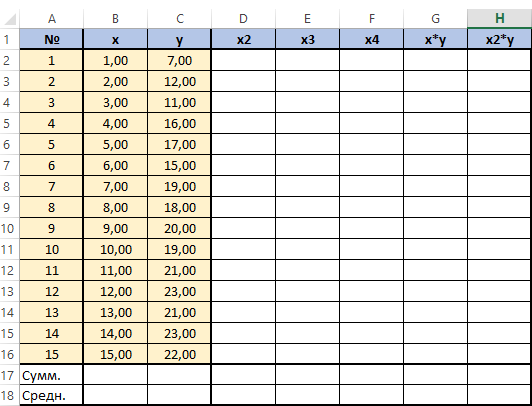
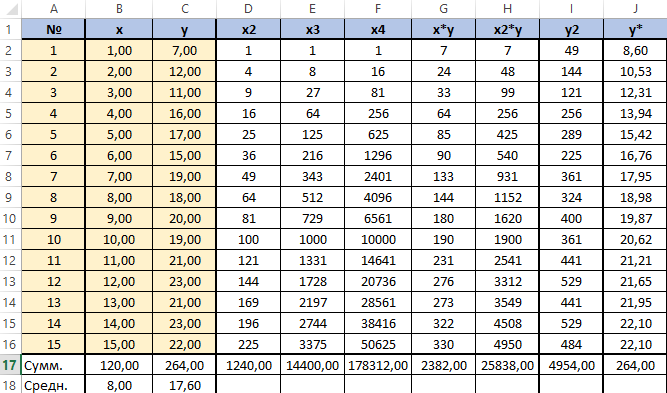
Получится заполненная нужными для решения уравнения таблица вида.

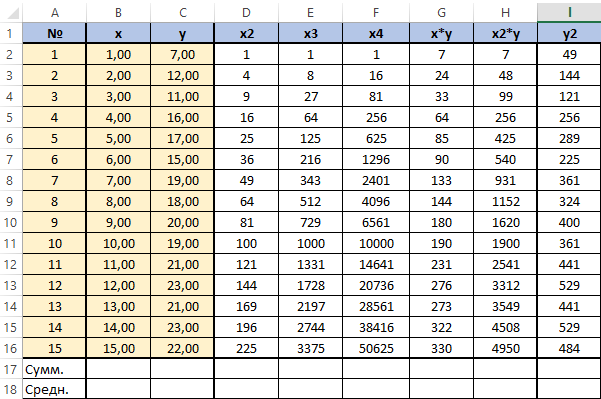
Далее посчитаем суммы по каждому столбцу - воспользуемся ∑ в программе Excel.

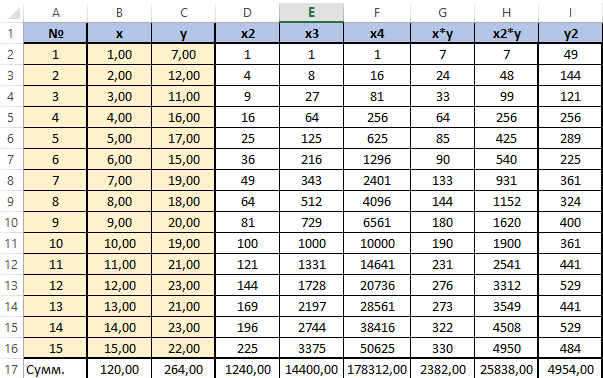
Сформируем матрицу A системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём "А=". Следуем той системе уравнений, которую мы избрали для решения регрессии.

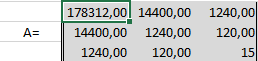
То есть, в ячейку B21 мы должны поместить сумму столбца, где возводили показатель X в четвёртую степень - F17. Просто сошлёмся на ячейку - "=F17". Далее нам необходима сумма столбца где возводили X в куб - E17, далее идём строго по системе. Таким образом, нам необходимо будет заполнить всю матрицу.

В соответствии с алгоритмом Крамера наберём матрицу А1, подобную А, в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. То есть сумма столбца X в квадрате умноженная на Y, сумма столбца XY и сумма столбца Y.

Также нам понадобятся ещё две матрицы - назовём их А2 и А3 в которых второй и третий столбцы будут состоять из коэффициентов правых частей уравнений. Картина будет такова.

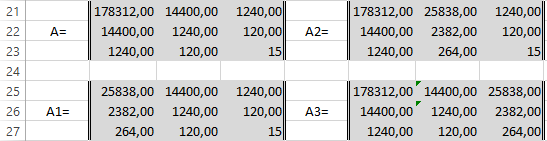
Следуя избранному алгоритму, нам нужно будет вычислить значения определителей (детерминантов, D) полученных матриц. Воспользуемся формулой МОПРЕД. Результаты разместим в ячейках J21:K24.

Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a (в ячейке M22) - "=K22/K21"; b (в ячейке M23) - "=K23/K21"; с (в ячейке M24) - "=K24/K21".

Получим наше искомое уравнение парной квадратичной регрессии:

y=-0,074x²+2,151x+6,523

Оценим тесноту линейной связи индексом корреляции.

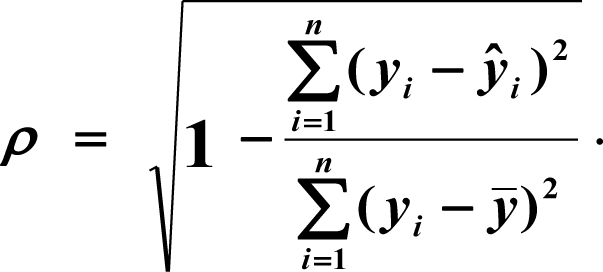
Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) - "=$m$22*B2*B2+$M$23*B2+$M$24". Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.

Для вычисления сумм (Y-Y усредненное)² добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.

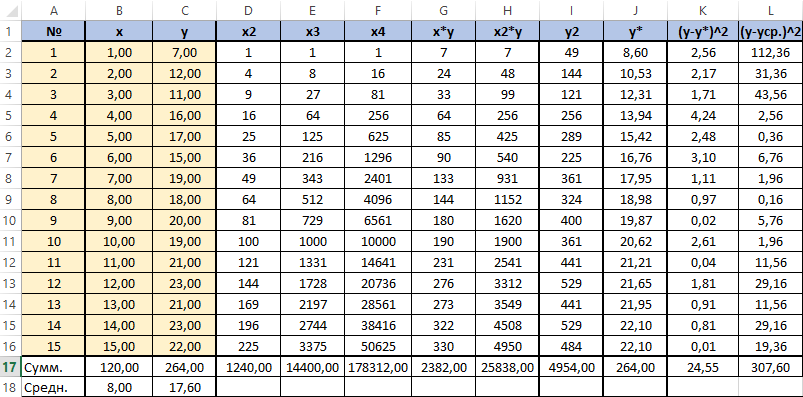
В ячейке K25 разместим формулу подсчёта индекса корреляции - "=КОРЕНЬ(1-(K17/L17))".

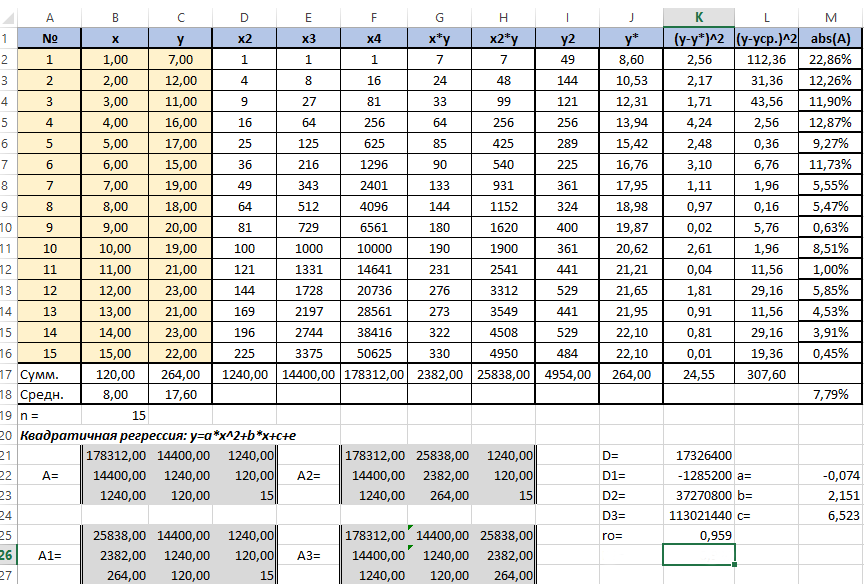
Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь.

Осталось оценить качество подгонки полученного квадратичного уравнения регрессии (индекс детерминации). Он рассчитывается по формуле квадрата индекса корреляции. То есть формула в ячейке K26 будет очень проста - "=K25*K25".

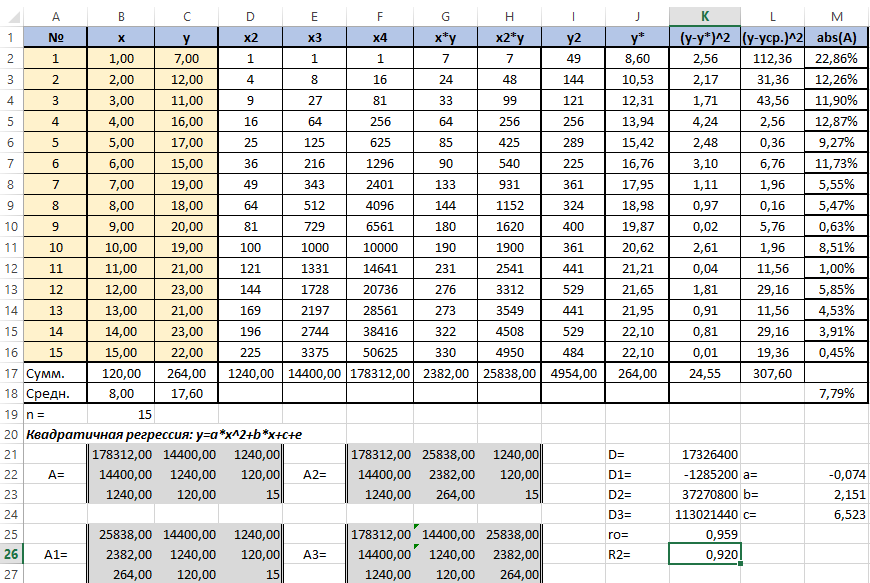
Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.

Последним действием будет вычисление относительной ошибки. Добавим столбец и внесём туда формулу: "=ABS((C2-J2)/C2), ABS - модуль, абсолютное значение. Протянем маркером вниз и в ячейке M18 выведем среднее значение (СРЗНАЧ), назначим ячейкам процентный формат. Полученный результат - 7,79% находится в пределах допустимых значений ошибки <8…10%. Значит вычисления достаточно точны.

Если возникнет необходимость, по полученным значениям мы можем построить график.

Файл с примером прилагается - ССЫЛКА!